Tetraédrico por sexta vez

Aunque me causa alegría haber llegado a los 35 años hoy, me da un poco de tristeza hacerlo lejos de mi país y de mi familia. Pero todo sea por darles algo mejor a ambos.

Si uno construye pirámides con base triangular acomodando naranjas, puede uno usar $1$, $4$, $10$, $20$, $35$, etcétera, de ellas. Es la sucesión de los números tetraédricos.

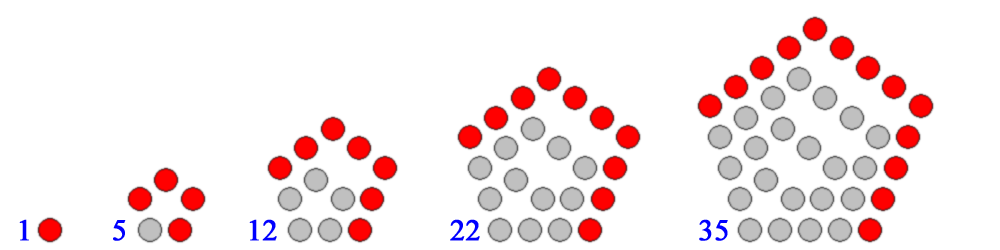
También es posible desmontar la sexta pirámide y armar justamente el sexto de los números pentagonales. Según las soluciones de la curva elíptica $Y^3+Y=X^{3}-X$, los únicos números tetraédricos con los que es posible hacer esto son $0$, $1$ y $35$.

Obviamente esto me sirve de pretexto para mencionar a mi héroe Euler y su teorema de los números pentagonales. Una última propiedad que encontré agradable del $35$ es que también es un coeficiente binomial. Más especificamente, es $$\binom{7}{4}=\binom{7}{3}=35$$ o sea, todas las formas de elegir (sin importar el orden) cuatro objetos entre siete disponibles. O de descartarlos, si se quiere. También esto significa que hay (sin tomar en cuenta equivalencias debidas a simetrías afines) la misma cantidad de acordes de tres que de cuatro notas en una escala diatónica.